帕斯卡三角

• Pascal’s Triangle
• Approach

Pascal’s Triangle

LeetCode 118

Given an integer numRows, return the first numRows of Pascal’s triangle.

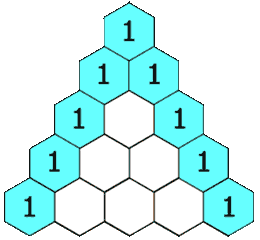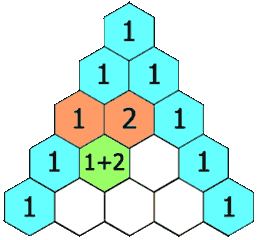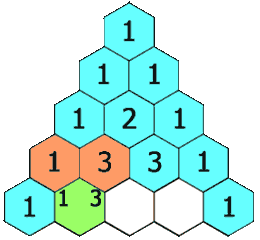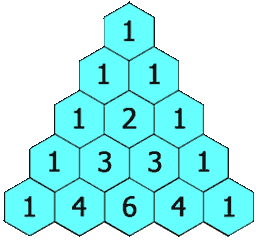
In Pascal’s triangle, each number is the sum of the two numbers directly above it as shown:

Example 1:

Input: numRows = 5
Output: [[1],[1,1],[1,2,1],[1,3,3,1],[1,4,6,4,1]]

Example 2:

Input: numRows = 1
Output: [[1]]

Constraints:

• 1 <= numRows <= 30

Approach

首先抛出结论：帕斯卡三角的 第 row 行第 col 个数，对应的正是 组合数 C(row, col)

下面我们来证明：
C(n, k) 表示从 n 个元素中选 k 个的方式数。

设这 n 个元素是：\({e_1, e_2, ..., e_n}\)，我们特别关注最后一个元素 \(e_n\)。

分两种情况：

• 选中了 \(e_n\)，那么还要从前 n-1 个元素中选 k-1 个：C(n-1, k-1)
• 没选 \(e_n\)，那么所有 k 个元素都要从前 n-1 个元素中选：C(n-1, k)

所以 C(n, k) = C(n-1, k-1) + C(n-1, k)

而这正是帕斯卡三角的每一项等于“左上 + 右上”的定义，即斯卡三角的 第 row 行第 col 个数等价于从 row 个元素里边选出 col 个元素的组合数量。

由组合公式可知，帕斯卡三角的 第 row 行第 col 个数：

这样就可以使用累乘器递增 col 计算第 row 行的每一个元素：

class Solution {
    fun generate(numRows: Int): List<List<Int>> = List(numRows) { row ->
        (1..row).runningFold(1) { acc, col ->
            acc.times(row - col + 1).div(col)
        }
    }
}

当然，这道题最容易想到的方法是使用前一行数按照帕斯卡三角的定义计算出当前行的数。
我们这里的重点是阐述帕斯卡三角和组合的等价关系，并使用组合公式计算任意位置的数。