problem A
Matthew is given two strings 𝑎 and 𝑏, both of length 3. He thinks it’s particularly funny to create two new words by swapping the first character of 𝑎 with the first character of 𝑏. He wants you to output 𝑎 and 𝑏 after the swap.
Note that the new words may not necessarily be different.
Input
The first line contains 𝑡 (1≤𝑡≤100) — the number of test cases.
The first and only line of each test case contains two space-separated strings, 𝑎 and 𝑏, both of length 3. The strings only contain lowercase Latin letters.
Output
For each test case, after the swap, output 𝑎 and 𝑏, separated by a space.
Example
input
6
bit set
cat dog
hot dog
uwu owo
cat cat
zzz zzz
output
sit bet
dat cog
dot hog
owu uwo
cat cat
zzz zzz
solution
fun main() {
repeat(readln().toInt()) {
solve()
}
}
fun solve() {
val a = readln().toCharArray()
val c = a[0]
a[0] = a[4]
a[4] = c
println(String(a))
}
problem B
Given an integer 𝑛, find an integer 𝑥 such that:
- 2≤𝑥≤𝑛.
- The sum of multiples of 𝑥 that are less than or equal to 𝑛 is maximized. Formally, 𝑥+2𝑥+3𝑥+⋯+𝑘𝑥 where 𝑘𝑥≤𝑛 is maximized over all possible values of 𝑥.
Input
The first line contains 𝑡 (1≤𝑡≤100) — the number of test cases.
Each test case contains a single integer 𝑛 (2≤𝑛≤100).
Output
For each test case, output an integer, the optimal value of 𝑥. It can be shown there is only one unique answer.
Example
input
2
3
15
output
3
2
Note
For 𝑛=3, the possible values of 𝑥 are 2 and 3. The sum of all multiples of 2 less than or equal to 𝑛 is just 2, and the sum of all multiples of 3 less than or equal to 𝑛 is 3. Therefore, 3 is the optimal value of 𝑥.
For 𝑛=15, the optimal value of 𝑥 is 2. The sum of all multiples of 2 less than or equal to 𝑛 is 2+4+6+8+10+12+14=56, which can be proven to be the maximal over all other possible values of 𝑥.
solution
fun main() {
repeat(readln().toInt()) {
println(solve())
}
}
fun solve(): Int {
val n = readln().toInt()
return if (n == 3) 3 else 2
}
problem C
Alex thinks some array is good if there exists some element that can be represented as the sum of all other elements (the sum of all other elements is 0 if there are no other elements). For example, the array [1,6,3,2] is good since 1+3+2=6. Furthermore, the array [0] is also good. However, the arrays [1,2,3,4] and [1] are not good.
Alex has an array \(𝑎_1,𝑎_2,…,𝑎_𝑛\). Help him count the number of good non-empty prefixes of the array 𝑎. In other words, count the number of integers 𝑖 (1≤𝑖≤𝑛) such that the length 𝑖 prefix (i.e. \(𝑎_1,𝑎_2,…,𝑎_𝑖\)) is good.
Input
The first line of the input contains a single integer 𝑡 \((1≤𝑡≤10^4)\) — the number of test cases.
The first line of each test case contains a single integer 𝑛 \((1≤𝑛≤2⋅10^5)\) — the number of elements in the array.
The second line of each test case contains 𝑛 integers \(𝑎_1,𝑎_2,…,𝑎_𝑛 (0≤𝑎_𝑖≤10^9)\) — the elements of the array.
It is guaranteed that the sum of 𝑛 over all test cases does not exceed \(2⋅10^5\).
Output
For each test case, output a single integer — the number of good non-empty prefixes of the array 𝑎.
Example
input
7
1
0
1
1
4
1 1 2 0
5
0 1 2 1 4
7
1 1 0 3 5 2 12
7
1000000000 1000000000 1000000000 1000000000 1000000000 1000000000 294967296
10
0 1000000000 1000000000 1000000000 1000000000 1000000000 1000000000 1000000000 1000000000 589934592
output
1
0
3
3
4
1
2
Note
In the fourth test case, the array has five prefixes:
- prefix [0] is a good array, as mentioned in the statement;
- prefix [0,1] is not a good array, since 0≠1;
- prefix [0,1,2] is not a good array, since 0≠1+2, 1≠0+2 and 2≠0+1;
- prefix [0,1,2,1] is a good array, since 2=0+1+1;
- prefix [0,1,2,1,4] is a good array, since 4=0+1+2+1.
As you can see, three of them are good, so the answer is 3.
solution
fun main() {
repeat(readln().toInt()) {
println(solve())
}
}
fun solve(): Int {
val n = readln().toInt()
val a = readln().split(' ').map(String::toLong)
var sum = 0L
var max = 0L
var cnt = 0
a.forEach {
max = max.coerceAtLeast(it)
sum += it
cnt += if (sum == 2 * max) 1 else 0
}
return cnt
}
problem D
Given a 𝑛 by 𝑚 grid consisting of ‘.’ and ‘#’ characters, there exists a whole manhattan circle on the grid. The top left corner of the grid has coordinates (1,1), and the bottom right corner has coordinates (𝑛,𝑚).
Point (𝑎,𝑏) belongs to the manhattan circle centered at (ℎ,𝑘) if |ℎ−𝑎|+|𝑘−𝑏|<𝑟, where 𝑟 is a positive constant.
On the grid, the set of points that are part of the manhattan circle is marked as ‘#’. Find the coordinates of the center of the circle.
Input
The first line contains 𝑡 (1≤𝑡≤1000) — the number of test cases.
The first line of each test case contains 𝑛 and 𝑚 \((1≤𝑛⋅𝑚≤2⋅10^5)\) — the height and width of the grid, respectively.
The next 𝑛 lines contains 𝑚 characters ‘.’ or ‘#’. If the character is ‘#’, then the point is part of the manhattan circle.
It is guaranteed the sum of 𝑛⋅𝑚 over all test cases does not exceed \(2⋅10^5\), and there is a whole manhattan circle on the grid.
Output
For each test case, output the two integers, the coordinates of the center of the circle.
Example
input
6
5 5
.....
.....
..#..
.....
.....
5 5
..#..
.###.
#####
.###.
..#..
5 6
......
......
.#....
###...
.#....
1 1
#
5 6
...#..
..###.
.#####
..###.
...#..
2 10
..........
...#......
output
3 3
3 3
4 2
1 1
3 4
2 4
solution
fun main() {
repeat(readln().toInt()) {
solve()
}
}
fun solve() {
val (n, m) = readln().split(' ').map(String::toInt)
val a = Array(n) { charArrayOf() }
repeat(n) {
a[it] = readln().toCharArray()
}
var top = Int.MAX_VALUE
var left = Int.MAX_VALUE
var right = 0
var bottom = 0
a.forEachIndexed { index, chars ->
chars.forEachIndexed { i, c ->
if (c == '#') {
top = top.coerceAtMost(index)
bottom = bottom.coerceAtLeast(index)
left = left.coerceAtMost(i)
right = right.coerceAtLeast(i)
}
}
}
println("${(top + bottom) / 2 + 1} ${(left + right) / 2 + 1}")
}
problem E
Ntarsis has a box 𝐵 with side lengths 𝑥, 𝑦, and 𝑧. It lies in the 3D coordinate plane, extending from (0,0,0) to (𝑥,𝑦,𝑧).
Ntarsis has a secret box 𝑆. He wants to choose its dimensions such that all side lengths are positive integers, and the volume of 𝑆 is 𝑘. He can place 𝑆 somewhere within 𝐵 such that:
- 𝑆 is parallel to all axes.every corner of 𝑆 lies on an integer coordinate.
- 𝑆 is magical, so when placed at an integer location inside 𝐵, it will not fall to the ground.
Among all possible ways to choose the dimensions of 𝑆, determine the maximum number of distinct locations he can choose to place his secret box 𝑆 inside 𝐵. Ntarsis does not rotate 𝑆 once its side lengths are selected.
Input
The first line consists of an integer 𝑡, the number of test cases (1≤𝑡≤2000). The description of the test cases follows.
The first and only line of each test case contains four integers 𝑥,𝑦,𝑧 and 𝑘 (1≤𝑥,𝑦,𝑧≤2000, 1≤𝑘≤𝑥⋅𝑦⋅𝑧).
It is guaranteed the sum of all 𝑥, sum of all 𝑦, and sum of all 𝑧 do not exceed 2000 over all test cases.
Note that 𝑘 may not fit in a standard 32-bit integer data type.
Output
For each test case, output the answer as an integer on a new line. If there is no way to select the dimensions of 𝑆 so it fits in 𝐵, output 0.
Example
input
7
3 3 3 8
3 3 3 18
5 1 1 1
2 2 2 7
3 4 2 12
4 3 1 6
1800 1800 1800 4913000000
output
8
2
5
0
4
4
1030301
Note
For the first test case, it is optimal to choose 𝑆 with side lengths 2, 2, and 2, which has a volume of 2⋅2⋅2=8. It can be shown there are 8 ways to put 𝑆 inside 𝐵.
The coordinate with the least 𝑥, 𝑦, and 𝑧 values for each possible arrangement of 𝑆 are:
- (0,0,0)
- (1,0,0)
- (0,1,0)
- (0,0,1)
- (1,0,1)
- (1,1,0)
- (0,1,1)
- (1,1,1)
The arrangement of 𝑆 with a coordinate of (0,0,0) is depicted below:
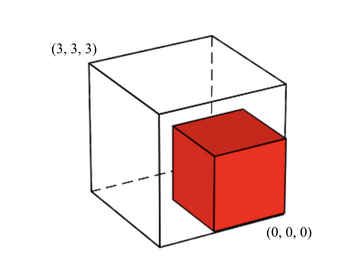
For the second test case, 𝑆 with side lengths 2, 3, and 3 are optimal.
solution
fun main() {
repeat(readln().toInt()) {
println(solve())
}
}
fun solve(): Long {
val (x, y, z, k) = readln().split(' ').map(String::toLong)
var ans = 0L
for (ix in 1..x) {
if (k.mod(ix) != 0L) continue
for (iy in 1..y) {
if (k.mod(ix * iy) != 0L) continue
val iz = k.div(ix * iy)
if (iz in 1..z) {
val curr = (x - ix + 1) * (y - iy + 1) * (z - iz + 1)
ans = ans.coerceAtLeast(curr)
}
}
}
return ans
}
problem F
You are facing the final boss in your favorite video game. The boss enemy has ℎ health. Your character has 𝑛 attacks. The 𝑖’th attack deals \(𝑎_𝑖\) damage to the boss but has a cooldown of \(𝑐_𝑖\) turns, meaning the next time you can use this attack is turn \(𝑥+𝑐_𝑖\) if your current turn is 𝑥. Each turn, you can use all attacks that are not currently on cooldown, all at once. If all attacks are on cooldown, you do nothing for the turn and skip to the next turn.
Initially, all attacks are not on cooldown. How many turns will you take to beat the boss? The boss is beaten when its health is 0 or less.
Input
The first line contains 𝑡 \((1≤𝑡≤10^4)\) – the number of test cases.
The first line of each test case contains two integers ℎ and 𝑛 \((1≤ℎ,𝑛≤2⋅10^5)\) – the health of the boss and the number of attacks you have.
The following line of each test case contains 𝑛 integers \(𝑎_1,𝑎_2,...,𝑎_𝑛 (1≤𝑎_𝑖≤2⋅10^5)\) – the damage of your attacks.
The following line of each test case contains 𝑛 integers \(𝑐_1,𝑐_2,...,𝑐_𝑛 (1≤𝑐_𝑖≤2⋅10^5)\) – the cooldown of your attacks.
It is guaranteed that the sum of ℎ and 𝑛 over all test cases does not exceed \(2⋅10^5\).
Output
For each test case, output an integer, the minimum number of turns required to beat the boss.
Example
input
8
3 2
2 1
2 1
5 2
2 1
2 1
50 3
5 6 7
5 6 7
50 3
2 2 2
3 3 3
90000 2
200000 200000
1 1
100000 1
1
200000
6 7
3 2 3 2 3 1 2
6 5 9 5 10 7 7
21 6
1 1 1 1 1 1
5 5 8 10 7 6
output
1
3
15
25
1
19999800001
1
21
Note
For the first test case, you can use attacks 1 and 2 on the first turn, dealing 3 damage in total, and slaying the boss.
For the second case, you can beat the boss in 3 turns by using the following attacks:
Turn 1: Use attacks 1 and 2, dealing 3 damage to the boss. The boss now has 2 health left.
Turn 2: Use attack 2, dealing 1 damage to the boss. The boss now has 1 health left.
Turn 3: Use attack 1, dealing 2 damage to the boss. The boss now has −1 health left. Since its health is less than or equal to 0, you beat the boss.
For the sixth test case: remember to use 64-bit integers as the answer can get large.
solution 1
import java.util.TreeSet
fun main() {
repeat(readln().toInt()) {
println(solve())
}
}
fun solve(): Long {
var (h, n) = readln().split(' ').map(String::toInt)
val a = readln().split(' ').map(String::toInt).toIntArray()
val c = readln().split(' ').map(String::toInt).toIntArray()
val treeSet = TreeSet(compareBy<Pair<Long, Int>> { it.first }.thenBy { it.second })
repeat(n) { treeSet.add(Pair(1L, it)) }
var turn = 1L
while (h > 0) {
val (t, i) = treeSet.first()
h -= a[i]
turn = t
treeSet.remove(treeSet.first())
treeSet.add(Pair(t + c[i], i))
}
return turn
}
solution 2
fun main() {
repeat(readln().toInt()) {
println(solve())
}
}
fun solve(): Long {
val (h, n) = readln().split(' ').map(String::toLong)
val a = readln().split(' ').map(String::toInt).toIntArray()
val c = readln().split(' ').map(String::toInt).toIntArray()
var l = 0L
var r = 1e11.toLong()
while (l < r) {
val mid = (l + r).shr(1)
var sum = 0L
for (i in a.indices) {
sum += a[i] * ((mid - 1 + c[i]) / c[i])
if (sum >= h) break
}
if (sum >= h) {
r = mid
} else {
l = mid + 1
}
}
return l
}
problem G
Let 𝐷(𝑛) represent the sum of digits of 𝑛. For how many integers 𝑛 where \(10^𝑙≤𝑛<10^𝑟\) satisfy 𝐷(𝑘⋅𝑛)=𝑘⋅𝐷(𝑛)? Output the answer modulo \(10^9+7\).
Input
The first line contains an integer 𝑡 (1≤𝑡≤104) – the number of test cases.
Each test case contains three integers 𝑙, 𝑟, and 𝑘 \((0≤𝑙<𝑟≤10^9, 1≤𝑘≤10^9)\).
Output
For each test case, output an integer, the answer, modulo \(10^9+7\).
Example
input
6
0 1 4
0 2 7
1 2 1
1 2 3
582 74663 3
0 3 1
output
2
3
90
12
974995667
999
Note
For the first test case, the only values of 𝑛 that satisfy the condition are 1 and 2.
For the second test case, the only values of 𝑛 that satisfy the condition are 1, 10, and 11.
For the third test case, all values of 𝑛 between 10 inclusive and 100 exclusive satisfy the condition.
solution
private const val M = (1e9 + 7).toLong()
fun main() {
repeat(readln().toInt()) {
println(solve())
}
}
fun solve(): Long {
val (l, r, k) = readln().split(' ').map(String::toLong)
val b = 9 / k + 1L
return (powMod(b, r, M) - powMod(b, l, M) + M).mod(M)
}
// Iterative Function to calculate (x^y)%m in O(log y)
fun powMod(x: Long, y: Long, m: Long): Long {
var x = x.mod(m)
if (x == 0L) return 0L
var y = y
var res = 1L
while (y > 0) {
if (y and 1 == 1L) {
res = mulMod(res, x, m)
}
x = mulMod(x, x, m)
y = y.shr(1)
}
return res
}
// Iterative Function to calculate (x*y)%m in O(log y)
fun mulMod(x: Long, y: Long, m: Long): Long {
var x = x
var y = y
var res = 0L
while (y > 0) {
if (y and 1 == 1L) {
res = (res + x).mod(m)
}
x = x.shl(1).mod(m)
y = y.shr(1)
}
return res
}