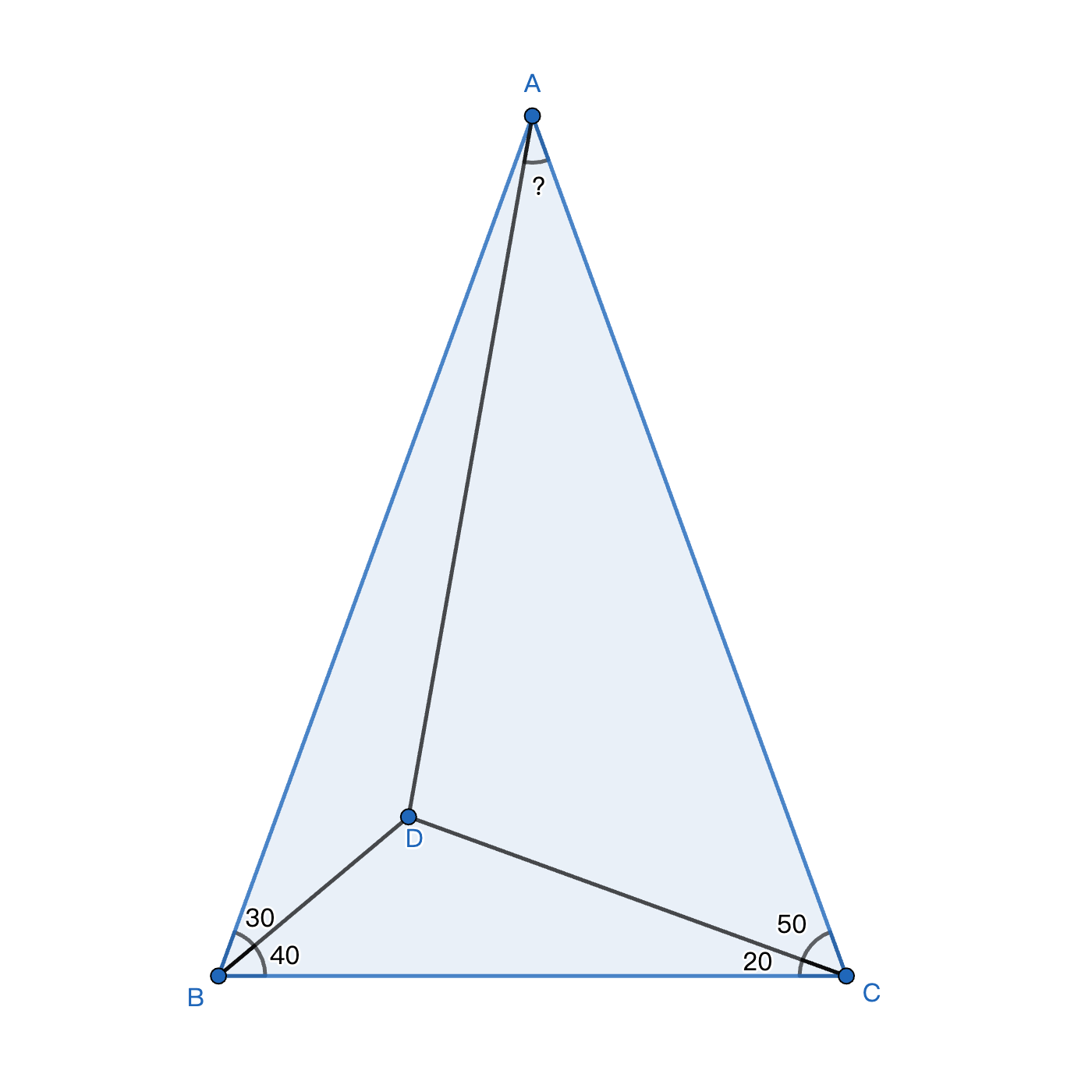
已知 ∠ABD=30°、∠CBD=40°、∠ACD=50°、∠BCD=20°,求∠CAD多少度?
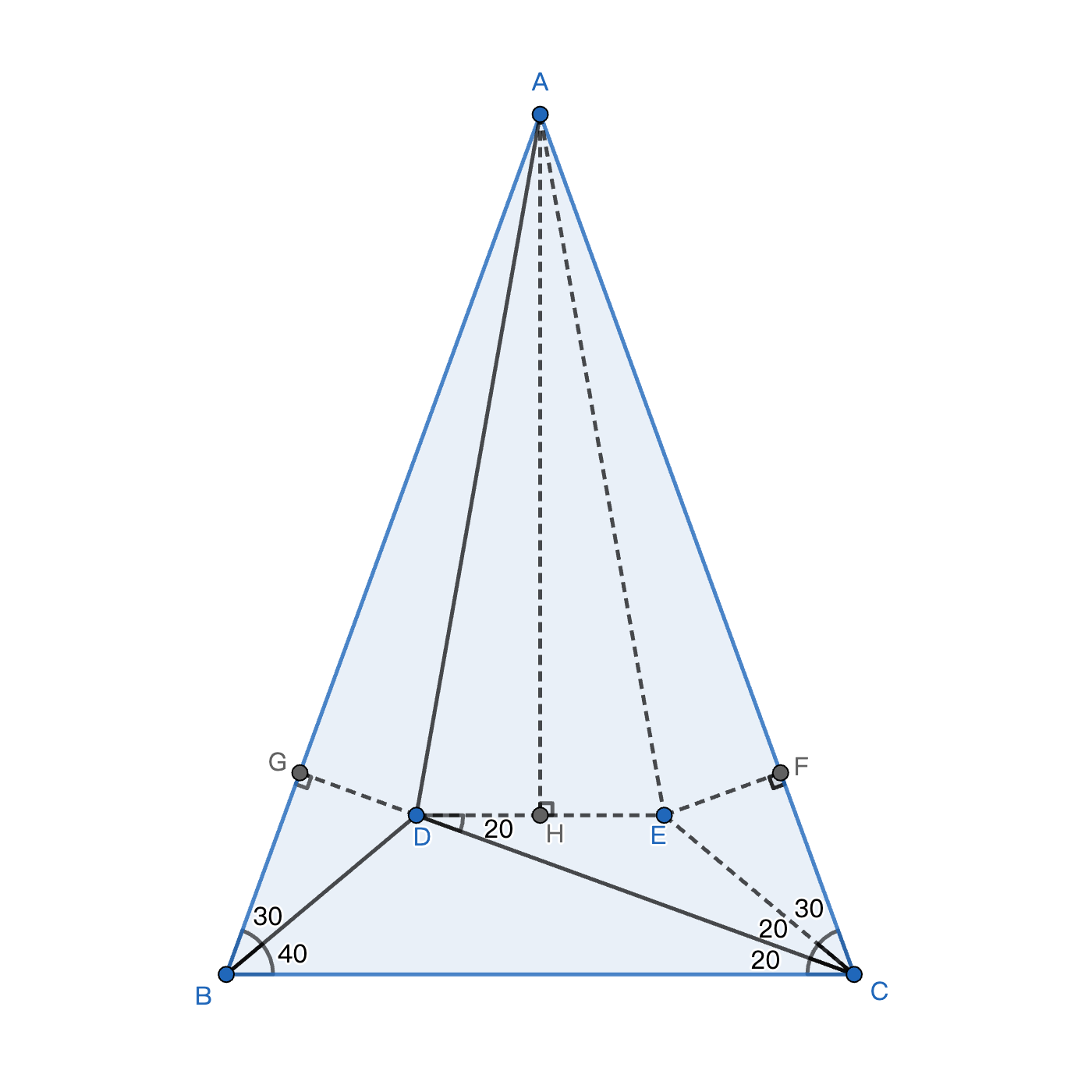
- 设辅助点 E,使得满足 DE//BC,∠DCE=20°,显然点 E 存在且唯一
- 过点 E 作 AC 垂直线相交点 F
- 过点 A 作 DE 垂直向相交点 H
- 延长 CD 与 AB 相交点 G,三角形内角和 180° ⇒ ∠BGC=90°,故 CG 垂直于 AB
∠ECF=∠ACD-∠ECD=30°、sin30°=1/2 ⇒ EC=2EF
∠DBC=40°=∠ECB、DE//BC ⇒ 四边形 DBCE 为等腰梯形 ⇒ BD=CE
∠DBG=30°、DG 垂直于 BG ⇒ BD=2DG
DE//BC,故 ∠EDC=∠BCD=20°=∠ECD ⇒ △ECD 为等腰三角形 ⇒ EC=ED
∠ABC=70°=∠ACB ⇒ △ABC 为等腰三角形 ⇒ AB=AC
AB=AC、∠ABD=30°=∠ACE、BD=CE ⇒ △ABD≌△ACE ⇒ AD=AE
AD=AE、∠AHD=∠AHE=90° ⇒ △AHD≌△AHE ⇒ DH=EH=1/2ED=1/2EC=1/2BD=EF=DG ⇒ △AGD≌△AHD≌△AHE≌△AFE
故 ∠CAD=∠FAD=3/4∠FAG=30°